Tính khoảng cách giữa 2 đường thẳng chéo nhau bằng CASIO

Xin chào tất cả các bạn, hôm nay mình sẽ hướng dẫn các bạn cách tính khoảng cách giữa hai đường thẳng chéo nhau.

Về cơ bản thì chúng ta sẽ có 2 hướng để tiếp cận: Một là dựa vào tích có hướng (note) và tích vô hướng, hai nữa là dựa vào ma trận.

Trong bài viết này mình sẽ tiếp cận theo hướng thứ 2, tức là dựa vào ma trận. Cụ thể hơn là ma trận $2 \times 2$ và $3 \times 3$

Việc tiếp cận theo hướng này sẽ gây ra chút khó khăn cho các bạn học sinh, tuy nhiên trắc nghiệm đang là xu hướng và máy tính CASIO ngày càng có nhiều tính năng hữu ích hơn => vậy nên khó khăn trên sẽ không hề đáng ngại phải không nào.

Mục Lục Nội Dung

#1. Công thức tính khoảng cách giữa hai đường thẳng chéo nhau

Trong không gian $Oxyz$ cho hai đường thẳng chéo nhau $(d)$ và $(d’)$. Tính khoảng cách giữa hai đường thẳng trên biết …

• $(d)$ đi qua điểm $M_0=(x_0; y_0; z_0)$ và có véc-tơ chỉ phương $\vec{u}=(a_1; b_1; c_1)$
• $(d’)$ đi qua điểm $M_0’=(x_0’; y_0’; z_0’)$ và có véc-tơ chỉ phương $\vec{u’}=(a_1’; b_1’; c_1’)$

Khoảng cách giữa hai đường thẳng $(d)$ và $(d’)$ được xác định bởi công thức:

$\frac{\left|\left|\begin{array}{ccc} a_1 & b_1 & c_1 \\ a_1′ & b_1′ & c_1′ \\ x_0′-x_0 & y_0′-y_0 & z_0′-z_0 \end{array}\right|\right|}{\sqrt{\left|\begin{array}{ll} b_1 & c_1 \\ b_1′ & c_1′ \end{array}\right|^2+\left|\begin{array}{ll} c_1 & a_1 \\ c_1′ & a_1′ \end{array}\right|^2+\left|\begin{array}{ll} a_1 & b_1 \\ a_1′ & b_1′ \end{array}\right|^2}}$

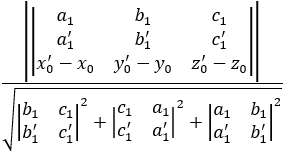
#2. Tìm hiểu thêm về cách chứng minh công thức

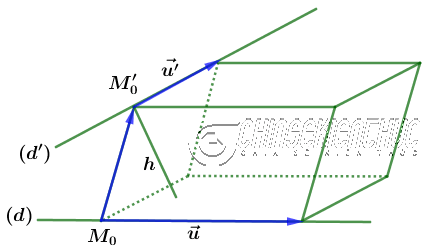
Gọi V là thể tích của hình hộp được tạo bởi $\vec{u}, \vec{u’}, \overrightarrow{M_0M_0′}$

Lúc bấy giờ V được tính theo công thức $[\vec{u}; \vec{u’}] \cdot \overrightarrow{M_0M_0′}=\left|\left|\begin{array}{ccc} a_1 & b_1 & c_1 \\ a_1′ & b_1′ & c_1′ \\ x_0′-x_0 & y_0′-y_0 & z_0′-z_0 \end{array}\right|\right|$

Gọi $S$ là diện tích của hình bình hành tạo bởi $\vec{u}, \vec{u’}$

Lúc bấy giờ S được tính theo công thức $[\vec{u}; \vec{u’}]=\sqrt{\left|\begin{array}{ll} b_1 & c_1 \\ b_1′ & c_1′ \end{array}\right|^2+\left|\begin{array}{ll} c_1 & a_1 \\ c_1′ & a_1′ \end{array}\right|^2+\left|\begin{array}{ll} a_1 & b_1 \\ a_1′ & b_1′ \end{array}\right|^2}$

=> Suy ra chiều của $h$ của hình hộp cũng chính là khoảng cách giữa hai đường thẳng chéo nhau và $h=\frac{V}{S}$

#3. Cách tính định thức của ma trận

3.1. Ma trận 2 x 2

Định thức của ma trận $A=\left(\begin{array}{ll}a&b\\c&d\end{array}\right)$ sẽ được tính theo công thức $a.d-c.b$

Chú ý: Định thức của ma trận A thường được kí hiệu là |A| hoặc Det(A)

3.2. Ma trận 3 x 3

Định thức của ma trận $B=\left(\begin{array}{lll}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{array}\right)$ sẽ được tính theo công thức

$a_{11}\left|\begin{array}{ll}a_{22}&a_{23}\\a_{32}&a_{33}\end{array}\right|-a_{12}\left|\begin{array}{ll}a_{21}&a_{23}\\a_{31}&a_{33}\end{array}\right|+a_{13}\left|\begin{array}{ll}a_{21}&a_{22}\\a_{31}&a_{32}\end{array}\right|$

#4. Ví dụ minh họa

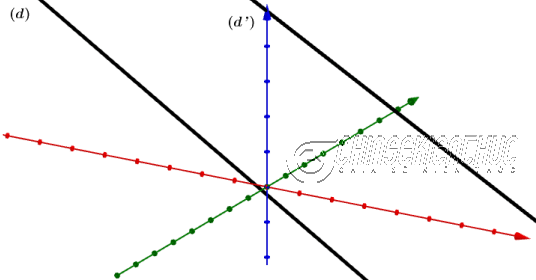
Tính khoảng cách giữa hai đường thẳng chéo nhau $(d):\frac{x}{2}=\frac{y-1}{1}=\frac{z+1}{-2}$ và $(d’):\frac{x-1}{1}=\frac{y-2}{2}=\frac{z-3}{-2}$

Lời Giải:

Dễ thấy …

• $M_0=(0; 1; -1)$ và $\vec{u}=(2; 1; -2)$ lần lượt là điểm đi qua và véc-tơ chỉ phương của đường thẳng (d)
• $M_0’=(1; 2; 3)$ và $\vec{u’}=(1; 2; -2)$ lần lượt là điểm đi qua và véc-tơ chỉ phương của đường thẳng (d’)

Suy ra $\overrightarrow{M_0M_0′}=(1; 1; 4)$

=> Vậy khoảng cách giữa $(d)$ và $(d’)$ là:

$\frac{\left|\left|\begin{array}{lll} 2 & 1 & -2 \\ 1 & 2 & -2 \\ 1 & 1 & 4 \end{array}\right|\right|}{\sqrt{\left|\begin{array}{ll} 1 & -2 \\ 2 & -2 \end{array}\right|^{2}+\left|\begin{array}{ll} -2 & 2 \\ -2 & 1 \end{array}\right|^{2}+\left|\begin{array}{ll} 2 & 1 \\ 1 & 2 \end{array}\right|^{2}}}=\frac{16\sqrt{17}}{17}$

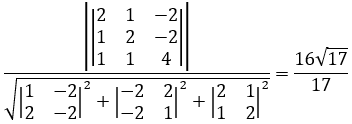
#5. Thủ thuật tính nhanh bằng máy tính CASIO fx-580VN X

Bước 1. Chọn phương thức tính toán Matrix

Bước 2. Lần lượt gán bốn ma trận vào MatA, MatB, MatC và MatD

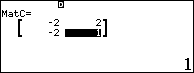
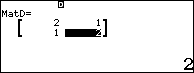
Bước 3. Tính giá trị biểu thức (Abs(Det(MatA))) ⨼(√((Det(MatB))²+(Det(MatC))²+(Det(MatD))²))

Chú ý ⨼ là phím phân số, √ là phím căn bậc hai

#6. Lời kết

Okay, đó là cách tính khoảng cách giữa hai đường thẳng chéo nhau mà theo mình là tối ưu nhất cho phần thi trắc nghiệm toán.

Nếu bạn là sinh viên thì cho dù câu hỏi được cho dưới dạng trắc nghiệm hay là tự luận đều không thành vấn đề, vì các bạn đã được học về ma trận trong chương trình Toán cao cấp hoặc Đại số tuyến tính.

Còn nếu bạn là học sinh và …

• Câu hỏi được cho dưới dạng trắc nghiệm thì hãy áp dụng công thức hoặc thủ thuật máy tính CASIO cho mình.
• Nếu câu hỏi được cho dưới dạng tự luận thì bạn hãy áp dụng công thức $\frac{|[\vec{u}; \vec{u’}] \cdot \overrightarrow{M_0M_0′} |}{|[\vec{u}; \vec{u’}]|}$

Hi vọng là bài viết sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com

Bài viết đạt: 5/5 sao - (Có 1 lượt đánh giá)

Note: Bài viết này hữu ích với bạn chứ? Đừng quên đánh giá bài viết, like và chia sẻ cho bạn bè và người thân của bạn nhé !

Adblock test (Why?)

Xem Them Chi Tiet

Nhung Mon Do Cong Nghe Duoc Yeu Thich

Do Cong Nghe Phu Kien
Xem Them Chi Tiet

Phu nu phai dep dan ong moi yeu! Sam ngay bo vay dam sieu dep

Thanh xuan nhu mot tach trá Khong mua do hot phi hoai thanh xuan